Краткое изложение содержания
Создатели страниц, в которых содержится спам, прибегают к различным технологиям для достижения высоких результатов в выдаче и быстрой раскрутки сайта. Есть специальные эксперты, которые умеют идентифицировать спам, но данный процесс достаточно трудоемкий и дорогостоящий. В связи с этим предлагается полуавтоматическая технология выявления спама. Сначала отбирается несколько случайных страниц, которые будут оценены экспертом. Идентифицировав вручную несколько случайно выбранных страниц, в дальнейшем используется ссылочная структура Интернета для определения других страниц, которые, скорее всего, окажутся «хорошими» и правильными страницами. В данной работе обсуждаются возможные способы случайного отбора и обнаружения «хороших» страниц. Представляются результаты экспериментов, проводимых в Интернете и оценка эффективности работы технологии. Результаты показали, что существуют эффективные способы фильтрации спама.
1. ВВЕДЕНИЕ
Термин "интернет-спам" используют для обозначения страниц, содержащих многочисленные ссылки, специально созданные для введения поисковых систем в заблуждение. Например, порнографический сайт может способствовать распространению спама в Интернете, добавляя тысячи ключевых слов на домашнюю страницу, причем текст зачастую специально делается невидимым для пользователей. Поисковая система индексирует дополнительные ключевые слова и предоставляет порнографическую страницу в качестве ответа на запросы, содержащие эти слова. Так как добавленные ключевые слова не являются непристойной лексикой, пользователи попадают на страницы такого сайта. Еще одна техника быстрой раскрутки сайта – создание большого количества поддельных веб-страниц, указывающих на единственную целевую страницу. В связи с тем, что многие поисковые системы учитывают количество входящих ссылок при ранжировании страниц, целевая страница, скорее всего, появится раньше всех в результатах поиска.
Вопрос, является ли страница или группа страниц спамом (это касается и электронной почты), достаточно субъективный. Например, возьмем несколько сайтов, неоднократно ссылающихся на страницы друг друга. Такие ссылки могут просто свидетельствовать о сходной тематике сайтов, или быть созданы специально для повышения ранжирования страниц. Зачастую достаточно проблематично определить, какой из двух сценариев раскрутки был использован.
В целом, пользователи легко распознают явные и неприкрытые проявления спама. Например, большинство согласится, что если основная часть текста на странице сайта невидима пользователю и не соответствует тематике, то, очевидно, страница была добавлена с намерением ввести поисковую систему в явное заблуждение. Точно так же дело обстоит, если на странице встречается огромное количество URL, ссылающихся на такие хосты как:- buy-canon-rebel-300d-lens-case.camerasx.com;
- buy-nikon-d100-d70-lens-case.camerasx.com;
- как помощь при тщательном изучении страниц на предмет спама;
- как способ борьбы с результатами спама.
Процесс алгоритмической идентификации спама сложен, поэтому схемы, представленные в данной работе не будут оперировать без вмешательства специалиста.
Предлагаемый алгоритм работает следующим образом: случайной выборкой избираются страницы, которые должны быть исследованы на наличие спама. Эксперт исследует «случайные страницы», и сообщает алгоритму, присутствует ли на них спам. Впоследствии алгоритм идентифицирует другие страницы, которые, скорее всего, окажутся «хорошими», при учете их связи с «хорошими случайными» страницами.
В этой работе:- Формализуется проблема веб-спама и алгоритма отслеживания спама.
- Определяются показатели оценки эффективности работы алгоритмов отслеживания спама.
- Представляются схемы для случайного отбора страниц, которые будут оценены вручную.
- Предлагается алгоритм TrustRank для определения вероятности «хороших» страниц.
- Обсуждаются результаты проведенной работы (роботы поисковой системы Alta Vista обошли 31 млн сайтов, 2 тыс. сайтов были изучены вручную). Предлагается любопытная статистика частоты встречаемости определенных видов контента.
2. ПРЕДВАРИТЕЛЬНАЯ ИНФОРМАЦИЯ
2.1. интернет-модель
Представляем модель сети в виде графа ς = (ν,ε),состоящего из множества ν страниц N и множества ε направленных ссылок, соединяющих страницы. На практике интернет-страница p может содержать многочисленные HMTL гиперссылки на некую другую страницу q. В этом случае мы представляем эти многочисленные ссылки как единственную ссылку (p,q) є ε. Мы также удаляем внутренние ссылки. На рис.1 представлен очень простой Интернет граф, состоящий из 4 страниц и 4 ссылок.
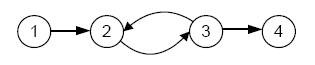
Каждая страница содержит входящие и исходящие ссылки. Количество входящих ссылок на страницу p представляет собой полустепень захода i(p). Количество исходящих ссылок – полустепень исхода w(p). Например, полустепень захода страницы 3 на рис.1 равна единице, а полустепень исхода – двум.
Страницы, которые не содержат входящие ссылки, называются страницами без ссылок. Страницы, которые не содержат исходящих ссылок, называются не ссылающимися страницами. Страницы, которые не содержат ни входящих, ни исходящих ссылок, называются изолированными. Страница 1 на рис.1 является страницей без ссылок, а страница 4 – не ссылающейся.Рассмотрим 2 матрицы интернет-графов, которые в дальнейшем будут иметь важное значение. Одна из матриц – матрица перехода Т:
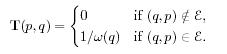
Матрица перехода, соответствующая графу на рис.1:
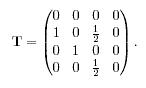
Рассмотри также обратную матрицу перехода U:
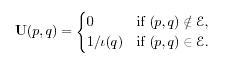
Необходимо обратить внимание, что U≠TT . Например, на рис.1 обратная матрица перехода выглядит так:
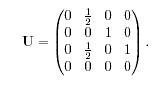
2.2. PageRank – алгоритм расчета авторитетности страницы, а также сам показатель в численном выражении. Так как предлагаемые алгоритмы основаны на PagеRank, в данном разделе предлагается его короткий обзор.Page Rank страницы будет достаточно высоким, если необходимое количество важных страниц указывают на эту страницу. Page Rank основывается на взаимном влиянии страниц. Страница не только сама оказывает влияние на другую страницу, но и испытывает влияние на себе. Показатели Page Rank r(p) страницы p определяются так:
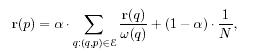
где α – коэффициент распада. Равносильно матричное уравнение:
Таким образом, оценка некоторой страницы p представляет сумму двух компонентов. Одна часть оценки относится к страницам, которые указывают на страницу p. Другая (статическая) часть оценки подходит для всех веб-страниц.
Page Rank может вычисляться итерационно, например, с помощью метода Jacobi. В строго математическом смысле итерация должна переходить в конвергенцию. На практике принято использовать четко зафиксированное число итераций.
Стандартный алгоритм PageRank присваивает статическую оценку каждой странице, версия Page Rank со смещением функционирует по-другому. В матричном уравнении
вектор d может быть использован для присвоения нулевой статической оценки ряду страниц. Оценка таких специальных страниц распространяется во время итерации на указываемые страницы.
3. ОЦЕНКА СТЕПЕНИ ДОВЕРИЯ
3.1. Функции прогнозирования и доверия
В разделе 1 уже было сказано, что распознавание спама – задача, требующая вмешательства человека и его субъективной оценки. Существует понятие проверки страницы на спам с помощью двоичной функции прогнозирования (О) всех страниц p є ν:
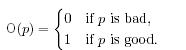
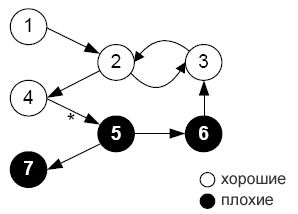
На рис.2 представлены 7 интернет-страниц. «Хорошие» страницы представлены на белом фоне, «плохие» – на черном. Вызывая функцию прогнозирования для страниц 1-4, будет выдано значение 1.
Процедура прогнозирования дорогостоящая и достаточно длительная. Поэтому применение подобной функции для всех страниц не приемлемо. При проведении анализа важно продемонстрировать избирательность, поэтому логичнее обратиться к эксперту для анализа некоторых интернет-страниц.
При анализе «хороших» страниц мы полагались на эмпирическое наблюдение:«Хорошие» страницы редко указывают на «плохие».Данный вывод основан на интуиции: «Плохие» страницы создаются с намереньем ввести поисковые системы в заблуждение, они далеки от цели предоставления полезной информации. Таким образом, у людей, создающих «хорошие» страницы, нет ни малейшего основания ссылаться на «плохие» страницы.
Однако создателей «хороших» страниц тоже иногда вводят в заблуждение. Поэтому в Интернете можно встретить ссылки с «хороших» страниц на «плохие» (на рис.2 такая ссылка показана между страницами 4 и 5 и помечена звездочкой). Рассмотрим пример. Возьмем хорошую, но немодерируемую гостевую книгу. Спамеры могут разместить ссылку на свои спам-страницы, как часть «невинных» сообщений, размещаемых в этой «гостевой».
Иногда спамерские сайты представляют из себя т.н. «Honeypot» («горшочек меда»): сайты представляют собой набор страниц, которые содержат полезную информацию (например, копии документации Unix), в то же время на страницах содержатся скрытые ссылки на спам-страницы. «Honeypot», привлекая пользователей ссылаться на них, увеличивает ранжирование страниц, содержащих спам.
Необходимо подчеркнуть, что, в свою очередь, заспамленные страницы часто ссылаются на «хорошие» страницы. Например, создатели заспамленных страниц указывают на «хорошие» и важные страницы, с целью создания «Honeypot», либо в надежде, что большое количество исходящих ссылок будут способствовать повышению некоторых видов ранжирования.Для оценки страниц, не прибегая к показателю О, необходимо оценить, какова вероятность того, что данная страница Р является «хорошей». Выражаясь научным языком, определяется функция доверия Т имеющая диапазон значений от 0 (плохая страница) до 1 (хорошая страница) В идеале, для любой страницы р, Т(р) должно показывать вероятность того, что страница р – «хорошая».
Идеальный показатель функции доверия
T(p) = Pr[O(p) = 1]
Допустим, имеется 100 страниц, показатель доверия которых составляет 0.7. Предположим, что оценка страниц осуществляется с использованием функции прогнозирования. Тогда, если Т сработает нужным образом, для 70 страниц показатель прогнозирования составит 1, а для оставшихся 30 – 0.
Если Т не может точно определить вероятность того, что страница «хорошая», то данная функция все равно окажется необходимой при делении страниц на «хорошие» и «плохие», полагаясь при этом на приблизительные данные. Например, даны две страницы, p и q. Показатель доверия страницы р ниже показателя доверия страницы q. Из этого следует, что вероятность того, что страница р «хорошая» ниже вероятности того, что страница q «хорошая». Функция доверия Т окажется полезной, по крайней мере, при распределении результатов поиска, когда предпочтение отдается страницам, которые, вероятнее всего, являются «хорошими».
Одним из предпочтительных свойств функции доверия является «свойство упорядоченности доверия»Один из способов понизить требования к показателю доверия – ввести пороговую величину δ.
Пороговый показатель функции доверия
Если страница p получает оценку выше показателя δ это свидетельствует о том, что страница «хорошая». В противном случае, о странице p ничего нельзя будет сказать. Функция Т предоставляет информацию, в соответствии с которой можно определить, что страницы, находящиеся в некотором подмножестве и имеющие высокий показатель доверия являются хорошими.
Обратите внимание, что функция Т с пороговым показателем не всегда влияет на сортировку страниц по принципу «хорошие»-«плохие».
3.2. Показатели оценки
В данном разделе представлены 3 показателя, которые помогают оценивать характеристики функции Т.
Допустим, имеется χ случайных интернет-страниц, для которых можно привлечь функции Т и О и оценить, как работают те или иные свойства для данного множества. (в разделе 6 будет рассказано, по какому принципу выбираются страницы, а пока мы считаем, что χ – множество случайных веб-страниц).Первый показатель тесно связан с заданным показателем доверия. Вводится двоичная функция I(T, O, p, q), с помощью которой определяется, что «плохие» страницы получили показатель доверия равный или выше «хороших» страниц
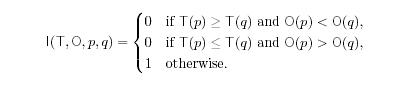
Затем из выборки χ страниц составляются множества 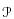 пар страниц (p,q), p ≠ q, затем вычисляется, с какими парами страниц функция доверия не допускает ошибок:
пар страниц (p,q), p ≠ q, затем вычисляется, с какими парами страниц функция доверия не допускает ошибок:
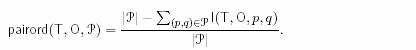 Pairwise Ordredness (упорядоченность пары)
Pairwise Ordredness (упорядоченность пары)
Если pairord равен 1, то в функции доверия ошибок не было, если pairord равен 0, то в функции доверия неправильная для всех пар.
Два следующих показателя относятся к пороговому показателю уровня доверия. Вводятся показатели precision (точности) и recall (воспроизведения) для пороговой величины δ. Показатель Precision вычисляется как отношение хороших страниц, принадлежащих χ, ко всем страницам, принадлежащим χ, показатель доверия которых указан.
Подобным образом, мы определяем показатель Recall как отношение количества хороших страниц с указанным показателем доверия к общему количеству хороших страниц, принадлежащих χ.
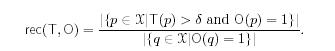
4. Вычисление доверия
В разделе 4.3 будет построен алгоритм TrustRank. Прежде необходимо произвести подготовительную работу.
Итак, приступим к выявлению функции доверия. Начнем с самого простого. При условии, что кол-во L ограничено для вычисления функции О, начнем непосредственно с выборки множества S случайных страниц L и вызовем функцию прогнозирования для заданных элементов. (В разделе 5 будет рассказано, как оптимально выбрать случайные страницы). Обозначим подмножества «хороших» и «плохих» страниц S+ и S- соответственно.Так как оставшиеся страницы не проверяются экспертами, им присваивается показатель доверия, равный ½ из-за отсутствия информации.
Вводится понятие пустая функция доверия T0 для любых p є ν:
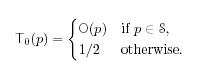
Например, присвоим L значение 3 и применим наш метод к примеру на рис.2 Случайно выбранное множество S может иметь значения {1, 3, 6}. Пусть o и t0 будут обозначать векторы прогнозирования и показателей доверия для каждой страницы соответственно. Тогда:
Для оценки поведения пустой функции доверия предположим, что наша выборка X состоит из 7 страниц, и и мы рассматриваем все возможные 42 (7*6) пары. Тогда показатель упорядоченности пары составит 17/21. Для порога δ =½ показатель precision составит 1, а показатель recall – ½.
4.1. Распространение функции доверия
Для дальнейшего подсчета показателя доверия воспользуемся несвязностью «хороших» страниц.
Случайным образом выбираем множество S из L страниц, которые будут подвержены прогнозированию. Предполагая, что «хорошие» страницы указывают на другие исключительно «хорошие» страницы, оценка 1 присваивается всем страницам, которые доступны в S+ множестве в М или менее переходов.
Соответствующая функция доверия TMопределяется так:
| M | pairord | prec | rec |
| 1 |
19/21
|
1
|
3/4
|
| 2 |
1
|
1
|
1
|
|
3
|
17/21
|
4/5
|
1
|
Таблица1: поведение М-шаговой функции доверия ТM, при M є {1, 2, 3} .
М-шаговая функция доверия
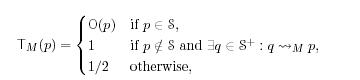
Где q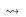 M p свидетельствует о существовании пути максимальной длины М со страницы q на страницу p. Такой путь не должен содержать «плохих» страниц.
M p свидетельствует о существовании пути максимальной длины М со страницы q на страницу p. Такой путь не должен содержать «плохих» страниц.
Используя пример на рис.2 и случайную совокупность S = {1, 3, 6}, можно представить оценку доверия для М с разными значениями:
M=1: t1 = [1, 1, 1, ½, ½, 0, ½]
M=2: t2 = [1, 1, 1, 1, ½, 0, ½]
M=3: t3 = [1, 1, 1, 1, 1, 0, ½]
В таблице1 показано, что при M = 1 и M = 2 значения pairord и recall возрастают, а значение precision равнo 1. Однако все совсем не так обстоит при M = 3. Страница 5 получает оценку 1 благодаря ссылке с «хорошей»страницы 4 на «плохую» страницу 5 (на рис. 2 отмечено звездочкой).Как показал предыдущий пример, проблема заключается в том, что при показателе доверия M-step нет абсолютной уверенности в том, что страницы из совокупности «хороших» страниц на самом деле являются «хорошими».
4.2. Затухание показателя доверия
Наблюдения свидетельствуют о том, что мы понижаем показатель доверия, по мере того, как все дальше и дальше удаляемся от «хороших» случайных страниц. Существует много способов по достижению снижения показателя доверия. Рассмотрим две возможные схемы.
На рис.3 предложен один из способов, который называется trust dampening (падение доверия). Так как страница 2 находится на расстоянии одной ссылки от «хорошей» случайной страницы 1, то ей можно присвоить заниженную оценку доверия β, где β Необходимо выбрать способ, как присваивать показатель доверия страницам, которые содержат многочисленные входящие ссылки. Например, на рис.3 стр.1 также ссылается на стр. 3. В этом случае, имеет смысл присвоить стр.3 максимальное значение показателя доверия, в данном случае β, или среднее значение, в данном случае: (β+β*β)/2
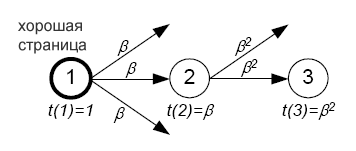
Второй способ для снижения показателя доверия, который называется trust splitting (разделение доверия) основан на следующем наблюдении: осторожность, с которой пользователи добавляют ссылки на свои страницы, обратно пропорциональна количеству ссылок на странице. Другими словами, если «хорошая» страница содержит всего несколько исходящих ссылок, то, скорее всего, страницы, на которые ведут эти ссылки, «хорошие». Однако если «хорошая» страница содержит сотни исходящих ссылок, то велика вероятность того, что страницы, на которые ведут эти ссылки, окажутся «плохими». Данное наблюдение приводит нас к «разделению доверия», так как данное наблюдение распространяется и на другие страницы: если страница р имеет показатель доверия Т(р) и указывает на !(р) страниц, то оценка для каждой из !(р) страниц будет равна отношению T(p)/!(p). В этом случае, реальная оценка страницы будет представлять собой сумму оценок, рассчитанных с помощью входящих ссылок. Наглядно, чем больше доверия получает страница с других страниц, тем больше вероятность того, что данная страница «хорошая».
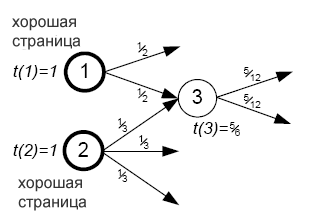
Рис.4 схематично представляет метод trust splitting. «Хорошая» случайная страница 1 содержит 2 исходящие ссылки, таким образом, она распределяет половину оценки, равной 1, между страницами, на которые она указывает. Точно так же, «хорошая» случайная страница 2 содержит три исходящих ссылки, соответственно, каждая страница, на которую указывает страница 2, получает одну треть от ее оценки. Тогда оценка страницы 3 будет складываться следующим образом: 1/2 + 1/3 = 5/6.
Необходимо отметить, что возможно совмещение двух способов снижения показателя доверия. На рис.4, например, стр.3 может быть присвоена оценка, которая рассчитывается следующим образом: β*(1/2 + 1/3) .В дальнейшем будет доказано, что при вычислении оценки доверия целесообразно полагаться на алгоритм Page Rank.
4.3 Алгоритм TrustRank
Функция TrustRank, изображенная на рис. 5, необходима при подсчете оценки доверия для интернет-графа. Алгоритм работы объясняется с помощью рис.2.
Алгоритм TrustRank представляет собой граф (переходная матрица Т и N интернет-страниц). Используются параметры, которые контролируют работу алгоритма (L, MB, αB см. ниже).

Шаг1: алгоритм вызывает функцию SelectSeed, которая возвращает вектор s. Составляющие вектора s(p) определяют «предпочтение» страницы p как случайной страницы (подробности можно найти в разделе 5). Как показано в разделе 5.1, одна версия SelectSeed возвращает следующий вектор к примеру на Рис.2:
Шаг 2: функция Rank(x,s) осуществляет преобразования вектора х в х', с элементами х'(i) в порядке убывания значения s(x’(i)). Например,
В соответствии с приведенным примером, страница 2 самая предпочтительная случайно выбранная страница, следующая 4 и т.д.
Шаг 3: активизируется функция Oracle для L, наиболее предпочтительных страниц. Составляющие статического вектора распределения d, соответствующие хорошим страницам, устанавливаются равными 1.Шаг 4: нормализуется вектор d, так, чтобы сумма его составляющих ровнялась 1. Допуская, что L=3, множество случайных страниц {2, 4, 5}. 2 и 4 являются хорошими случайно выбранными страницами, мы получаем следующий вектор распределения статических оценок для нашего примера,
Допуская, что αВ = 0,85, МВ = 20, алгоритм показывает следующий результат:
Из данного примера видно, что алгоритм TrustRank присваивает хорошим страницам более высокий показатель. В частности, три из четырех хороших страниц (2, 3 и 4) получили высокий показатель, а две из трех плохих страниц (страницы 6 и 7) получили низкий показатель. Однако, показатели страниц 1 и 5 были определены алгоритмом не адекватно. Страница 1 не была среди случайно выбранных и не имела достаточного количества ссылок с сайтов с высокими показателями, но ее показатель остался равным 0. Со всеми хорошими страницами, не имеющими ссылок, происходит тоже самое, если только они не случайно выбранные. Плохая страница 5 получила высокий показатель, т.к. на этой странице указана одна из редких good-to-bad ссылок. Как будет видно из раздела 6, несмотря на подобные ошибки, на реальном веб-графе алгоритм TrustRank правильно определяет большинство подходящих страниц.
5. Выбор случайных страниц
Задача функции SelectSeed определить предпочтительные страницы, которые войдут в случайно выбранные. Желательно найти страницы, которые будут наиболее пригодными для определения дополнительных подходящих страниц. В то же время желательно не увеличивать количество случайно выбранных страниц с целью ограничения использования функции Oracle. В данном разделе будут рассмотрены две стратегии для функции SelectSeed, как дополнение к ранее упомянутой стратегии случайного выбора.
5.1. Инверсный (обратный) PageRankТ.к. показатель доверия во многом определяется хорошими случайными страницами, одним из подходов может быть выбор страниц, с помощью которых будет возможно получить другие. В особенности, выбор случайных страниц, принимая во внимание исходящие ссылки. Например, на Рис.2, где соответствующее множество случайных страниц L=2, т.к. S = {2, 5}, у страниц 2 и 5 самое большое число исходящих ссылок.

В дальнейшем, можно увеличить покрывающую способность. Набор случайных страниц могут составить те страницы, которые указали большее количество страниц, в свою очередь, указавших на другие страницы и т.д. Интересно, что данный подход близок схеме, по которой работает PageRank, разница в том, что в нашем случае важность страницы зависит от ее исходящих ссылок, а не от входящих. Таким образом, чтобы рассчитать предпочтительность страницы, произведем вычисления PageRank на графе ς׳ = (ν,ε׳), где
Алгоритм называется инверсным, т.к. мы инвертировали ссылки. На рис.6 показан алгоритм вычислений инверсного PageRank. Заметьте, что коэффициент затухания αI и число итераций (переходов) MI могут отличаться от αB и МB, использованных в алгоритме TrustRank. Вычисления идентичны сделанным по традиционному алгоритму PageRank (Раздел 2.2), за исключением инверсной переходной матрицы U, использованной вместо обычной переходной матрицы Т.
Для нашего примера на рис.2, алгоритм инверсного PageRank (αI = 0,85, MI = 20) дает следующие показатели (уже продемонстрированные в Разделе 4.3):
Для числового значения L = 3, случайный набор S = {2, 4, 5}. Соответственно, подходящее случайное множество S+ = {2, 4}, т.о. страницы 2 и 4 являются отправной точкой для расчета распределения.
Важно помнить, что инверсный PageRank является эвристическим (хорошо функционирующим, что можно увидеть в Разделе 6). Во-первых, инверсный PageRank не гарантирует максимальный охват. Например, на рис.7, где L = 2, максимальная покрывающая способность распространяется либо на случайное множество {1, 3}, либо на {2, 3}. Хотя, вычисления инверсного PageRank демонстрируют следующий степенной вектор:
который ведет к случайному множеству S = {1, 2}.
Тем не менее, инверсный PageRank представляет интерес потому, что время выполнения его расчетов полиномиально, тогда как, определение максимального охвата является проблемой NP-полноты.
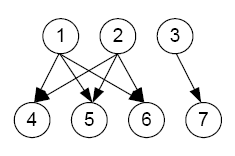
Во-вторых, увеличение охвата не всегда является наилучшей стратегией. Проиллюстрируем это, распространяя показатель доверия посредством разделения, без учета каких-либо его сокращений. Возвращаясь к Рис.7, выбираем страницу 2 как случайную, она оказывается хорошей. Затем страницы 4, 5 и 6, каждая получает показатель 1/3. Предположим, что случайно выбранная страница 3 также будет хорошей. Страница 7 получает показатель 1. В зависимости от конечной цели, предпочтительным может быть использование страницы 3, т.к. можно точно предположить какие страницы она определит, несмотря на то, что их может быть немного. Однако если использовать показатель доверия лишь для сравнения с другим показателем, следует рассмотреть большее количество страниц пусть с меньшей точностью.
5.2. Высокий PageRank
Допустим, что степень идентификации страниц, как хороших или плохих, будет одинаковой для всех веб-страниц. Более важным может оказаться доказательство того, что страница, имеющая высокую оценку среди результатов поиска, действительно является хорошей. Например, контенты страниц p, q, r и s адекватно и в равной степени отвечают введенному запросу. Если поисковая система использует PageRank для упорядочивания результатов, то страница с самым высоким PageRank например, p, будет представлена первой, затем страница с меньшим PageRank – q и т.д. в порядке убывания. Вероятнее, что пользователя заинтересуют страницы p и q, а не r и s, поэтому в первую очередь необходимо определить показатель доверия для страниц p и q. Например, если страница p окажется спамерской, то пользователь может воспользоваться страницей q.Таким образом, второе подтверждение эвристичности PageRank в выборе случайного набора страниц заставит отдать предпочтение страницам с высоким PageRank, так как такие страницы укажут на достойные их страницы. Следовательно, можно будет определить соответствующие показатели доверия страниц, занимающих первые строки в результатах поиска. Выбор случайных страниц согласно PageRank предоставит возможность определить, насколько подходящей является страница (по сравнению с инверсным PageRank). Но эти страницы потребуют более тщательного рассмотрения.
6. ЭКСПЕРИМЕНТЫ
6.1. Комплект данных
С целью вычисления алгоритмов были проведены эксперименты (август 2003) с использованием полного множества страниц, найденных и проиндексированных поисковой системой Alta Vista.
Для сокращения вычислительных затрат, работа будет проведена на уровне сайтов, а не отдельных страниц (следует отметить, что все представленные методы подходят как для сайтов, так и для страниц). Несколько миллиардов страниц было сгруппировано в 31 003 946 сайтов с помощью специального алгоритма, который является частью Alta Vista. Все отдельные страницы с одинаковыми доменными именами были объединены в один сайт. Решив проводить эксперимент на уровне сайтов, была сделана одна ссылка с сайта a на сайт b, тогда как на оригинальном веб-графе одна или более ссылок со страниц сайта а на страницы сайта b.
Для данных вычислений, один из авторов этой работы сыграл роль оракула, исследуя страницы различных сайтов, проверяя их на спам и предлагая дополнительную классификацию, которая будет представлена далее. Но использование алгоритма оценки автора, может стать причиной необъективных результатов. Ручное вычисление показателя доверия заняло недели: проверка сайта состояла из просмотра большего количества страниц с целью выявления намерения обмануть поисковую систему. Следующей трудновыполнимой задачей было найти специалистов в области поисковых систем, которые смогли бы выполнить данное задание. Вместо этого, автор наблюдал за работой специалистов, изучая технику определения спамерских сайтов. В дальнейшем, им были предприняты попытки использования данных методов с последующим представлением максимально объективных результатов.
6.2. Множество случайно выбранных страниц
Первый этап был представлен экспериментами по сравнению инверсного PageRank и высокого PageRank (Раздел 5.1 и 5.2). Для скорейшего представления результатов, для проведения экспериментов были использованы комплексные веб-графы, представляющие основные характеристики сетевого спама. Принимая во внимание ограничения в объеме статьи, описание экспериментов не будет представлено полностью. Следует отметить лишь то, что использование инверсного PageRank для определения множества случайно выбранных страниц, представляется лучшим. Поэтому, все дальнейшие эксперименты будут проведены с использованием данного метода.Метод инверсного PageRank позволил выстроить весь процесс таким образом, чтобы дать правильную оценку прогнозирования. В первую очередь были представлены полные вычисления инверсного PageRank с помощью веб-графа на уровне сайтов, со следующими параметрами αI = 0,85 и МI = 20. (Коэффициент затухания, равный 0,85, впервые был заявлен в и с тех пор считается стандартной величиной в PageRank литературе. Тесты показывают, что 20 итераций было достаточно, чтобы достигнуть конвергенции на относительной упорядоченности сайтов.)
После упорядочивания сайтов на основании значения их инверсного PageRank (шаг(2) на Рис.5), основное внимание было уделено первым 25 000. Вместо полного вычисления прогноза для данных сайтов, сначала была произведена беглая оценка, для удаления некоторые сомнительных сайтов. В частности, было замечено, что сайты с высоким показателем инверсного PageRank демонстрируют большую предрасположенность к спаму, главным образом из-за клонов открытых каталогов: некоторые спамеры делают точные копии всего контента открытого каталога DMOZ, в надежде улучшить основные показатели или с намерением создать «Honeypot», о которых шла речь в разделе 3.1. Чтобы быстро избавиться от спама, из списка 25 000 сайтов были удалены те, которые не значились в крупнейших веб-каталогах, сократив первоначальный набор до 7 900 сайтов. Выборочная проверка отфильтрованных сайтов показала, что были удалены некоторые хорошие сайты.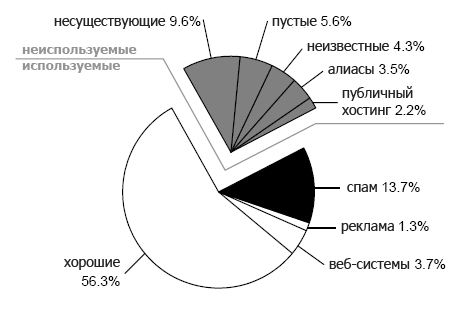
Из оставшихся 7 900 сайтов, оценке были подвергнуты первые 1 250 (множество случайно выбранных сайтов S), из которых подходящими были признанны 178. Данный процесс представлен на Рис.5, шаг (3). Относительно небольшое количество сайтов, составляющих случайное множество S+, стало результатом жесткого критерия отбора: сайты не только проверялись на спамерские, по отношению к ним, также, был использован второй фильтр. В соответствии с ним, отбирались сайты только с четко распознаваемым владельцем (такие как правительственные или образовательный учреждения и компании), осуществляющим контроль за контентом сайта. Дополнительный фильтр гарантировал продолжительную и качественную работу случайно выбранного множества сайтов.
6.3. Примерная оценка
Чтобы определить показатели, представленные в Разделе 3.2, необходимо множество χ сайтов с известными показателями прогнозирования. Было выбрано 1000 сайтов, данное количество сможет предоставить нужные данные и в достаточно короткий срок.
Было решено не выбирать сайты случайно. Т.к. многие сайты могли оказаться небольшими, содержать лишь несколько страниц и/или иметь очень низкий PageRank. Известно, что небольшие сайты и сайты с низким PageRank следуют распределению по степенной зависимости, зачастую оказываясь одними из последних. В соответствии с разделом 5.2, более важным представляется определение спама на сайтах с высоким PageRank, т.к. именно они чаще других фигурируют в результатах запроса. К тому же, представить точную оценку небольшому сайту сложнее из-за недостатка данных о нем.Чтобы обеспечить репрезентативность, был использован следующий метод. Сайты были расположены в убывающим порядке, согласно значению их PageRank, весь список был разделен на 20 блоков, каждый из которых включал разное количество сайтов, но с показателям PageRank в сумме равном 5%, от общего показателя PageRank.
Таким образом первый блок включал 86 сайтов с самыми высокими показателями, во втором блоке было 665, тогда как 20-ый состоял из 5 млн. сайтов с самыми низкими показателями.
Примерный набор из 1000 сайтов был составлен путем случайной выборки из каждого блока. Далее была проведена поверка сайтов с целью определения спамерских. Результаты представлены на Рис.8 – диаграмма, представляющая различные виды сайтов. Таким образом, было определено, что лишь 748 сайтов будут использованы для определения показателя TrustRank.- Хорошие. 563 сайта с качественными контентами и с нулевым или незначительным числом ссылок на спамерские сайты.
- Веб-системы. 37 сайтов, принадлежащих к системам, которые обеспечивают сохранение Всемирной сети (WWW), либо занимаются деятельностью, близкой к интернет-услугам. Все сайты хорошие, большинство ссылок автоматические. Эти сайты получили особую маркировку, чтобы упростить наблюдение за ними.
- Реклама. 13 сайтов функционировали как средства баннерной рекламы. Данные сайты не обладали полезным контентом, а их показатель PageRank основывался главным образом на получаемых ими автоматических ссылках. Тем не менее, они считаются хорошими сайтами, не представляющими спам.
- Спам. На 135 сайтах были обнаружены различные виды спама. Соответственно, они признаются плохими сайтами.
Эти 748 сайтов образуют множество χ. Оставшиеся 252 были признаны не пригодными для дальнейших вычислений по разным причинам:
- Публичный хостинг. 22 сайта размещали свои страницы. Большое количество независимых издателей, представляющих разнообразные контенты для этих сайтов, затруднили их определение как хороших или плохих. Следует отметить, что на уровне страниц не возникнет подобной трудности.
- Алиасы. У 35 сайтов были альтернативные адреса, они были лучше известны под другими именами. Такие сайты были исключены, т.к. важность алиаса не соответствует важности оригинального сайта.
- Пустые сайты. 56 сайтов были пустыми. Они состояли из одной страницы, которая не отличалась высоко информативностью.
- Несуществующие сайты. 96 сайтов считались несуществующими – либо они не были найдены в доменной системе имен, либо использованные системы не могли установить TCP/IP связь с соответствующими компьютерами.
- Неизвестные сайты. 43 сайта не удалось оценить на основе доступной информации. Главным образом это были Восточно-Азиатские сайты, на которых лишь незначительная часть контента была представлена на английском языке.
6.4. Результаты
В Разделе 4 были описаны способы передачи показателя доверия для множества случайно выбранных страниц. В этом разделе будут рассмотрены три альтернативных варианта TrustRank и две основные стратегии, и оценена их эффективность с помощью выборки χ:- TrustRank. На рис.5 представлены использованный алгоритм (МВ = 20 итераций и коэффициент затухания αВ = 0,85) и выбранные хорошие сайты (178).
- PageRank. Считается, что PageRank является самым лояльным к спаму показателем, потому что он оценивает лишь серьезные крупномасштабные изменения (незначительные изменения в структуре ссылки не оказывают влияния на показатель). Вопрос, как справляется PageRank со спамом сейчас, будет совершенно уместным. Поэтому в расчетах PageRank страницы «а» использовался как показатель для Т(а). Вновь М = 20 итераций с коэффициент затухания αВ = 0,85.
- Пустой Trust. За всеми сайтами был закреплен показатель пустого доверия равный ½, за исключением 1250 случайно выбранных сайтов с показателями 0 или 1.
6.4.1. PageRank против TrustRank
В первую очередь следует представить разницу между PageRank и TrustRank. Алгоритм PageRank не учитывает качество сайта, а возможные наказания сайта за не качественность точно не определены. Нередко сайты, созданные умелыми спамерами, получают высокий показатель PageRank. Тогда как TrustRank призван различать хорошие и плохие сайты: это дает надежду на то, что спамерские сайты не получат высоких показателей.
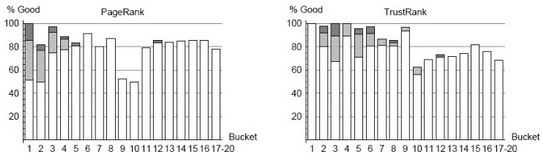
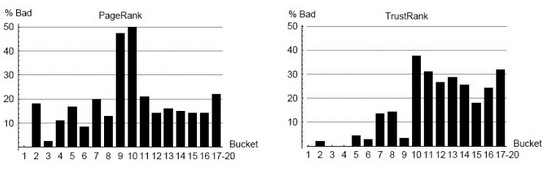
На рис.9 и рис.10 представлено сравнение PageRank и TrustRank с учетом плохих и хороших сайтов в каждом блоке. Блоки PageRank были представлены в разделе 6.3; было определено, что блоки TrustRank включают такое же число сайтов, что и блоки PageRank. Блоки с 17 по 20 были объединены и для PageRank, и для TrustRank. (Эти последние 4 блока включают более чем 13 млн. сайтов, не имеющих ссылок. Все такие сайты получили минимальный статический показатель PageRank и показатель нулевого TrustRank, предоставляя возможность упорядочить их).
Горизонтальные оси на рис.9 и 10 отмечают число блоков PageRank и TrustRank. Вертикальные оси на первом рисунке соответствуют процентному соотношению хороших сайтов в каждом блоке, число хороших сайтов деленное на общее число сайтов в блоке.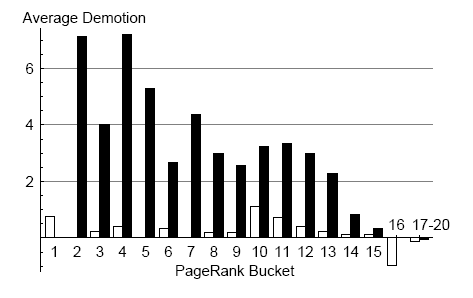
Следует помнить, что достойные сайты, сайты веб-систем, реклама рассматриваются как хорошие; относительное увеличение отмечена белым, светло-серым и темно-серым соответственно. Вертикальные оси второго рисунка соответствуют процентному соотношению плохих сайтов в определенном блоке. Например, согласно рис.10, 31% приемлемых сайтов в блоке TrustRank является плохим.
На данном рисунке видно, что TrustRank является приемлемым средством для выявления спама. Заметьте, что в первых пяти блоках TrustRank нет спама, тогда как в блоках, расположенных ниже отмечено высокое содержание спама. В то же время, удивительно, что второй блок PageRank почти на 20% считается плохим. Для PageRank, соотношение плохих сайтов достигло рекордного уровня в блоках 9 и 10 (50% спама).
Рис.11 предлагает другой взгляд на отношения PageRank и TrustRank. Здесь вводится понятие понижение(demotion), явление, когда сайт из блока с более высоким PageRank, появляется в блоке с более низким TrustRank. Отрицательное понижение это повышение(promotion), предполагающее обратный порядок действий: сайт из блока с низким PageRank появляется в блоке с более высоким TrustRank. Среднее понижение плохих сайтов – важный элемент вычисления TrustRank.
Горизонтальные оси на рис.11 соответствуют блокам PageRank. Вертикальные обозначают количество блоков, сайты которых из PageRank перемещались (понижались) в TrustRank. Белый цвет соответствует достойным сайтам, черный – спаму.
На рис.11 видно, что среди сайтов, занимающих высокие позиции, нет спама, это свидетельствует о эффективности TrustRank. Данный показатель демонстрирует и то, что хорошие сайты, в большинстве случаев, оставались в том же блоке, куда попали изначально. Следовательно, можно констатировать, что TrustRank (в отличие PageRank), гарантирует, что первые позиции будут занимать только хорошие сайты. К сожалению, из-за недостатка информации (внутренние ссылки) о сайте, TrustRank не может отличить хороший сайт с низким показателем от плохого.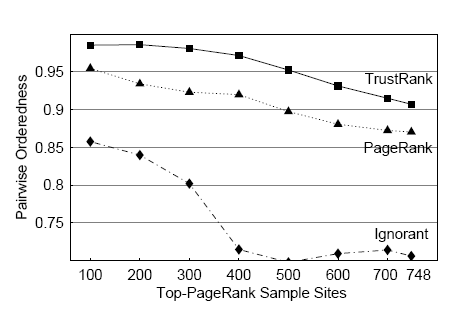
6.4.2. Pairwise orderedness (PO)
Данные PO, представленные в разделе 3.2, также используются для вычисления показателя TrustRank. Для проведения этого эксперимента был составлено множество  всех возможных пар сайтов для нескольких подмножеств случайной выборки Х. Чтобы проверить TrustRank для наиболее важных сайтов, используется подмножества χ, состоящее из 100 сайтов с самыми высокими показателями PageRank. Затем, постепенно, к подмножеству χ добавлялись сайты с меньшим PageRank. В конечном итоге, для вычисления показателя PO были использованы все пары из 748 сайтов.
всех возможных пар сайтов для нескольких подмножеств случайной выборки Х. Чтобы проверить TrustRank для наиболее важных сайтов, используется подмножества χ, состоящее из 100 сайтов с самыми высокими показателями PageRank. Затем, постепенно, к подмножеству χ добавлялись сайты с меньшим PageRank. В конечном итоге, для вычисления показателя PO были использованы все пары из 748 сайтов.
Результаты эксперимента показаны на рис.12. Горизонтальные оси указывают число сайтов, использованных для расчета, тогда как вертикальные оси представляют показатели PO для определенных сайтов. Например, для 500 сайтов с высоким PageRank, показатель PO для TrustRank будет равен приблизительно 0,95.
На рис.12 также изображены показатели PO для функции пустого Trust и PageRank. Совмещение множеств случайных выборок S и χ произошло на 5 хороших сайтах, от функции пустого Trustэти сайты получили показатели равные ½. Показатели PO для пустой функции используются в том случае, когда информации о качестве сайта минимальна. Также и для PageRank, показатели PO указывают, сколько имеется нужной информации для определения качеств сайта. Из данного примера видно, что TrustRank превосходит и пустую функцию и PageRank.
6.4.3. Показатели точность (Precision) и воспроизведение (Recall)Последние результаты эксперимента (рис.13) представляют определение TrustRank с учетом показателей Precision и Recall. Пограничные показатели TrustRank, отделяющие 17 блоков TrustRank, используются как пороговые значения δ, о которых говорилось в разделе 6.4.1. Последние блоки, соответствующие каждому пороговому значению, представлены на горизонтальных осях, на вертикальных показаны показатели Precision и Recall.
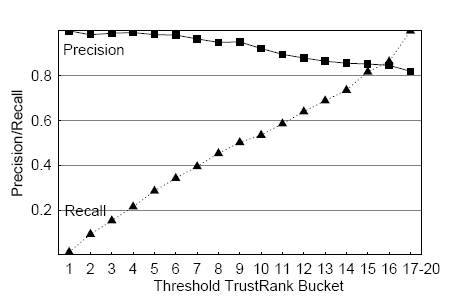
У хороших сайтов, согласно TrustRank, высокие показатели, соответственно, чем ниже показатель, теми хуже сайт. Таким образом, показатели Precision и Recall демонстрируют линейное понижение и повышение. Обратите внимание на высокий показатель Precision (0,82) для всего примерного множества: подобное значение не может быть общим для проблем традиционного поиска информации, обычно состоящих из большого объема документов, где лишь часть является подходящей определенному запросу. В отличие от этого, наше примерное множество состоит, главным образом, из хороших документов, все из которых подходящие. Вот почему базовый показатель Precision для множества χ такой 613/(613+135) = 0,82.
7. Заключение
С увеличением размеров и значения сети, роль поисковых систем становится все более значительной. Однако сейчас серьезной угрозой для поисковых систем стал сетевой спам возникающий в процессе быстрой и нечестной раскрутки сайта, из-за которого ухудшается функционирование различных сервисов. Для борьбы со спамом, поисковые системы используют различные методы. Проведенное в данной статье исследование стало одной из попыток формализовать проблему и представить ее комплексное решение. Согласно результатам эксперимента, возможно точно определять высококачественные хорошие страницы, не являющиеся спамом.
Несмотря на проделанный объем работы, пунктов, достойных более внимательного рассмотрения, осталось достаточно. В дополнение ко всему вышесказанному, следует отметить, что использованные методы могут быть улучшены. Например, вместо выбора всего случайного множества сразу, следует рассмотреть использование пошагового процесса. Это может стать темой будущих исследований.Обратите внимание, что существует несколько эквивалентных определений понятия PageRank, которые могут несущественно отличаться математической формулировкой и числовыми значениями, но представлять относительно одинаковую упорядоченность между думя веб-страницами.
Проблема определения минимального набора страниц, представляющих максимальную покрывающую способность, подобна проблеме независимого набора на направленном графе, как показано далее. Веб- графы могут быть трансформированы в направленные графы ς" = (ν,ε"), где ребро графа (p,q) є ε" показывает, что на страницу q можно попасть со страницы p. Спорно, что такая информация не внесёт никаких изменений в весь алгоритм, так как он включает обширный поиск с полиноминальным временем исполнения. Затем, нахождение минимального множества обеспечивает максимальный охват, который сходен с максимальным независимым множеством для ς", которое является проблемой NP-полноты.
Доменное имя – это часть URL, расположенная между префиксом http://, который называется схема и первым слэшом, который следует за высокоуровневым доменом, например, .com или TCP номером порта сервера. Например, доменное имя URL http://www.stanford.edu/db_pages/members.html – это www.stanford.edu.



 Теги:
Теги:
