Меня многие спрашивают, как оптимизаторы ставок считают вероятность конверсии на малых данных? И как при нескольких кликах на ключевое слово можно оценить конверсию? Постарался ответить на эти вопросы в статье.
Введение
Сами по себе клики с рекламы уже давно не интересуют рекламодателей. В самом простом случае рекламодателей интересует число конверсий. Поэтому перед тем как выставить ставки, нужно оценить какая доля кликов по ключевику закончится конверсией.
Конечно, есть и рекламодатели, которых интересует не только число конверсий, но и доход. Но ожидаемый доход на клик рассчитывается примерно по таким же принципам, как и конверсия.
Мы, конечно, можем просто взять показатель конверсии ключевика, однако это довольно неточная оценка. Например, если мы монетку подкинем 10 раз, то не всегда у нас будет 5 орлов и 5 решек. Также и показатель конверсии довольно сильно колеблется из недели к неделе в силу случайности.
Вероятность конверсии
Показатель конверсии и вероятность конверсии – это две большие разницы. Например, при 1 клике и 0 конверсий показатель нулевой. Но это не значит, что вероятность конверсии тоже нулевая, и никто никогда не конвертируется.
Показатель – это некоторое число, которое позволяет нам оценить вероятность конверсии. Чем больше у нас кликов, тем точнее показатель конверсии. Далее мы будем называть вероятность конверсии просто «конверсией».
Наша задача максимально точно оценить конверсию. Чем точнее мы это сделаем, тем больше конверсий сможем получить за те же деньги.
Комбинация оценок
Почти все современные алгоритмы машинного обучения используют принцип взвешенного голосования. Он довольно прост и хорошо вам знаком по некоторым видам спорта, КВН и конкурсам красоты.
Несколько судей выставляет оценки участнику, после чего считается итоговая оценка – как среднее между оценками судей. Например, 3 судьи поставили 7, 8 и 9, вычисляется средняя оценка (7+8+9)/3= 24/3=8.
Судьи, не всегда объективны, и их оценки не точны. Но с ростом числа судей повышается объективность (точность) оценки. Допустим, объективная оценка участника 7 баллов. Судья с вероятностью в 50% снижает оценку на 1 балл. С вероятность в 50% завышает на 1 балл. Средняя ошибка равна 1 баллу.
Если у нас есть 2 судьи, то возможны 4 равновероятных комбинации
|
Судья 1 |
Судья 2 |
Итого |
Ошибка |
|
6 |
6 |
6 |
1 |
|
6 |
8 |
7 |
0 |
|
8 |
6 |
7 |
0 |
|
8 |
8 |
8 |
1 |
В итоге средняя ошибка сократилась вдвое до 0,5 баллов. Другими словами, увеличение числа судей повышает точность итоговой оценки.
Веса
Все люди разные, и один судья может давать более точные оценки, чем другой. Это также можно учесть. Нужно взять не простое среднее, а средневзвешенное, где вес каждого судьи зависит от его объективности. Например, голос первого судьи считать за 2 голоса.
- E – финальная оценка
- E – оценки судей
- w – веса судей
- n – число судей
Свойства
При взвешивании итоговая оценка будет между исходными оценками, не больше максимальной и не меньше минимальной.
Если мы правильно подберем веса, то это повысит качество оценки. При хорошем подборе финальная оценка будет лучше, чем ее составляющие. Даже если множество оценок не намного лучше случайных, то финальная оценка будет намного лучше случайной.
Переобучение
Другое преимущество взвешенного голосования – отсутствие переобучения. Еще лет 15 назад в машинном обучении наблюдался парадокс: вычислительные мощности росли, но машины от этого не становились умнее. После некоторого уровня увеличение сложности алгоритма ухудшало качество прогноза. Этот эффект называется переобучением.
Однако, в конце 90-х обнаружили выход. Оказалось, что взвешенное голосование, снижает переобучение. Поэтому сейчас почти все алгоритмы машинного обучения используют взвешенное голосование.
Надежность
Но самое важное в нашем случае – это высокая надежность. Если одна из оценок имеет высокую погрешность, то это решается автоматически – просто снижением веса. При правильном подборе весов, взвешенное голосование будет давать адекватный результат, даже когда почти все оценки «выйдут из строя».
Даже если у ключевика нет кликов и нет показателя конверсии, у нас есть показатель конверсии объявления и сайта.
Парадокс Марковича
Многие из вас слышали о портфельной теории Марковича. Она рассказывает о том, как подбирать оптимальный инвестиционный портфель, обладающий самой высокой доходностью при заданном риске.
На первый взгляд, нужно все вложить в самую быстрорастущую компанию. Однако этот вариант очень рискованный – если она разорится, то мы все потеряем. Нужно диверсифицировать портфель, чтобы снизить риск.
Я против использования т.н. портфельной теории в контекстной рекламе, которая с теорией Марковича не имеет ничего общего. Однако в теории Марковича есть довольно примечательный парадокс.
Допустим есть 2 типа ценных бумаг, бумага Б явно хуже А: меньшая доходность и выше риск. В общем случае оптимальный инвестиционный портфель будет содержать обе ценные бумаги (естественно, доля бумаги А будет выше). Это происходит, поскольку общий риск снижается из-за диверсификации портфеля.
Примерно такой же парадокс существует и при взвешивании. Если есть две оценки: очень хорошая А и очень плохая Б, то оптимальный вес Б не будет равен нулю.
Эти два парадокса объясняются одной и той же формулой. Тоже происходит что-то вроде диверсификации рисков.
Контекстная реклама
Вернемся к контекстной рекламе. Как я уже говорил, показатель конверсии – оценка конверсии. Т.е. можно сказать что вероятность конверсии примерно равна показателю конверсии. Обозначим показатель как r, а вероятность как p:
Также мы можем сказать, что вероятность конверсии примерно равна показателю конверсии сайта (m).
Из чего получаем взвешенную оценку:
Веса (w) подбираются так, чтобы снизить погрешность итогового прогноза:
- вес показателя ключа зависит от числа кликов. Если число кликов нулевое, то он равен нулю и формула сводится просто к конверсии сайта.
- вес конверсии сайта зависит от того, насколько разная конверсия ключевых слов. Чем более разные ключевые слова, тем меньше вес m.
ПББ
Один из методов решения нашей задачи в матстатистике – это бета-биномиальная модель с определением априорной дисперсии по методу наибольшего правдоподобия. Для краткости мы будем его называть ПББ (Простейшая Бета-Биномиальная модель).
Это метод известен уже лет 50. Также он упомянут в патенте Marin Software. Хотя, возможно, в Marin Software сейчас использует другой алгоритм.
Бета-биномиальная модель
Случайные величины подчиняются некоторым законам распределениям. Закон говорит о том, какие значения встречаются чаще, а какие – реже. Например, людей среднего роста больше, чем очень высоких. Зная закон, мы можем сделать некоторые выводы. Например, если мы возьмем случайного человека, то с вероятностью в 95% его рост будет ниже двух метров.
У закона распределения есть 2 основных момента:
- Матожидание. Грубо говоря, среднее. Например, средний рост человека.
- Дисперсия – говорит о том, насколько разный рост у разных людей.
Из теории вероятностей известно, что число конверсий подчиняется биномиальному распределению с параметрами p (конверсия) и n (число кликов). Это записывается так:
Если мы возьмем случайный ключевик с сайта (о котором мы больше ничего не знаем), то его конверсия будет подчиняться некоторому закону. Как ни трудно догадаться, в бета-биномиальной модели считается конверсия подчинятся бета-распределению.
Где m – матожидание (средняя конверсия у ключевиков на сайте). Параметр A – это некоторая мера «одинаковости» конверсии у ключевиков. Он обратно зависит от дисперсии. Чем более разная конверсия у ключей, тем меньше А.
Допустим, мы знаем, что у ключевика было n кликов и s конверсий. Используя теорему Байеса, после долгих расчетов получим, что конверсия этого ключевика имеет следующее распределение:
Это наше представление о конверсии ключевика, сделанное на основе его данных и распределения ключевиков на сайте.
Матожидание этого распределения будет равно:
Эта формула говорит о средней конверсии ключевого слова, имеющего s конверсий и n кликов. Это искомая оценка конверсии.
Параметр А вычисляется методом наибольшего правдоподобия. Нужно подобрать такой А, который лучше всего соответствует данным сайта. Этот расчет довольно сложен и даже на компьютере занимает много времени. Для него нужно вычислить по 90 специальных математических функций (гамма и полигамма) на каждый ключевик.
Среднее взвешенное
Формула из прошлой главы это среднее взвешенное показателя сайта и ключевого слова с весами:
Чем более однородные ключи на сайте, тем сильнее учитывается показатель сайта. Чем больше кликов, тем сильнее в ней учитывается показатель ключа. При 0 числе кликов, наша оценка равна m, а при бесконечном – r.
Примеры
Допустим, у нас есть m=1%, посмотрим, какую оценку мы дадим.
|
Клики |
Конверсии |
Показатель |
A=1 |
A=2 |
A=3 |
|
0 |
0 |
нет |
1% |
1% |
1% |
|
1 |
0 |
0% |
0.99% |
0.995% |
0.997% |
|
1 |
1 |
100% |
1.98% |
1.49% |
1.33% |
|
10 |
0 |
0% |
0.91% |
0.95% |
0.97% |
|
10 |
1 |
10% |
1.82% |
1.43% |
1.29% |
|
10 |
10 |
100% |
10% |
5.7% |
4.19% |
|
100 |
0 |
0% |
0.5% |
0.66% |
0.75% |
|
100 |
1 |
1% |
1% |
1% |
1% |
|
100 |
2 |
2% |
1.5% |
1.33% |
1.25% |
|
100 |
10 |
10% |
5.5% |
4% |
3.25% |
|
1000 |
0 |
0% |
0.09% |
0.16% |
0.23% |
|
1000 |
10 |
1% |
1% |
1% |
1% |
|
1000 |
20 |
2% |
1.9% |
1.83% |
1.77% |
Как мы видим, на больших данных оценки не сильно отличаются от показателя. Но при малых данных взвешенные оценки адекватнее показателя конверсии.
Погрешность
Можно сравнить ошибки показателя конверсии и взвешенной оценки:
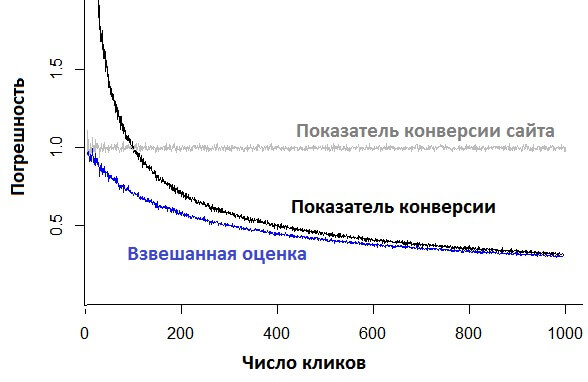
При малом числе кликов взвешенная оценка обладает в несколько раз меньшей погрешностью, но с ростом числа кликов точность обоих оценок становится примерно одинаковой.
Прибыль
Точность в швейцарский банк не положишь, поэтому смоделируем влияние погрешности на прибыль:
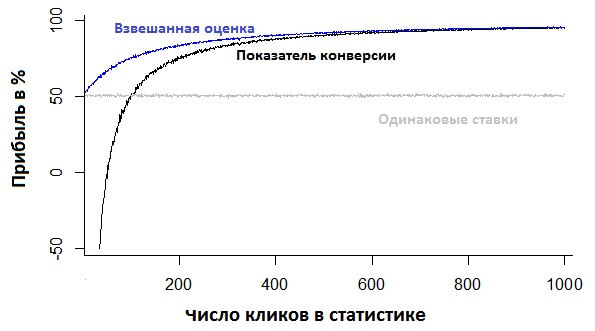
100% максимальная прибыль (при идеальном прогнозе). Как мы видим, при использовании взвешенной оценки прибыль всегда выше, чем при использовании показателя конверсии или выставлении одинаковых ставок.
MREM
Это небольшое улучшение ПББ, этот алгоритм работает в бесплатном онлайн калькуляторе конверсии.
Расчет m
Основная проблема ПББ в том, что m должно быть оценкой конверсии среднего ключевика, а не оценкой конверсии по сайту. Это разные вещи, поскольку у разных ключевых слов – разное число кликов.
Например, у нас есть 11 ключевых слов. В 10 из них по миллиону кликов, и показатель конверсии равен 2%, а в 11-ом 10 миллионов кликов и показатель конверсии равен 1%. Показатель конверсии сайта равен 1,5%, но конверсия среднего ключевика в районе 1.9%.
Эта проблема усугубляется еще и тем, что есть корреляция между числом кликов и конверсией. Т.е. конверсия зависит от частотности ключевика. Низкочастотники, обычно имеют большую конверсию. В силу чего m обычно занижен.
Даже если корреляции изначально нет, то она появляется при адекватной расстановке ставок, поскольку число кликов зависит от ставки, которая в свою очередь зависит от вероятности конверсии по ключевику.
В итоге, из-за этого оценка m методом ПББ обладает большой погрешностью, даже на очень больших данных, даже при бесконечном числе кликов и ключевых слов. Такие оценки в статистике называют несостоятельными. Такая погрешность в m приводит к тому, что точность оценки, особенно, низкочастотных ключевых слов снижается.
REM
Чтобы улучшить расчет m, обычно в матстатистике используют двухпараметрическую модель, когда методом наибольшего правдоподобия ищется не только А, но еще и m. Однако такая модель нестабильна на малых данных.
В качестве компромисса мы использовали REM (Random Effect Model) из Мета-анализа (раздела теории вероятностей). В MREM m считается по сложной формуле, в которой учитывается дисперсия. Это повышает точность вычисления m и стабилизирует расчет на малых данных.
При 100 ключевиках:
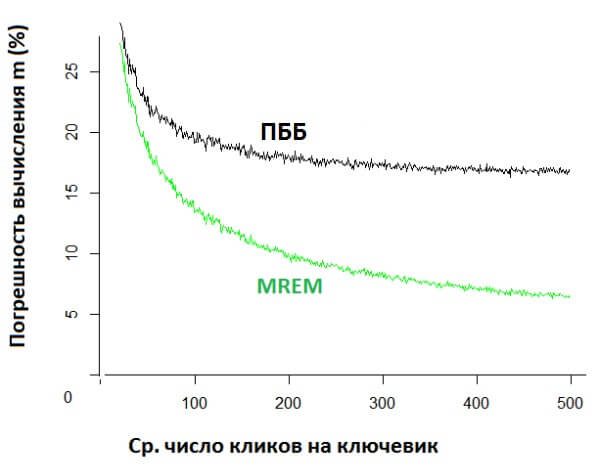
Как мы видим, после какого-то порога число кликов не улучшает оценку m по ПББ. Это связано с тем, что корреляция между кликами и конверсией рождает систематическую ошибку.
При 1000 ключевиках этот эффект еще заметнее:
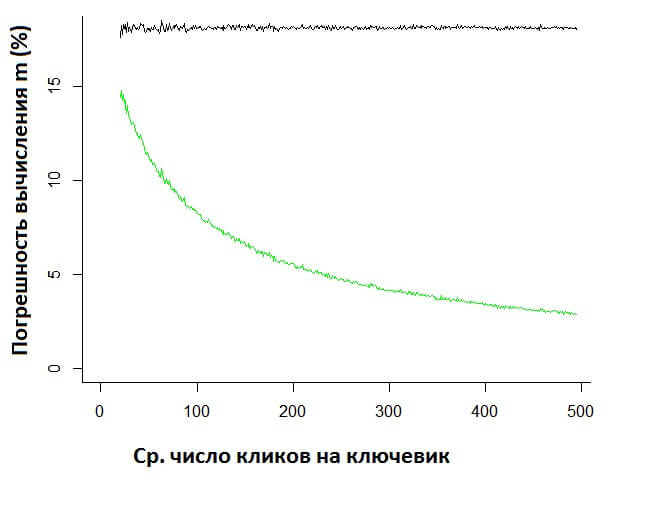
Как мы видим, погрешность Marin перестает зависеть от объема данных. Поскольку эта ошибка в основном связана не с малым объемом данных, а с проблемами модели.
Вес m
При использовании REM вес m теперь зависит не только от A и m, но еще и числа ключевиков на сайте, числа кликов у сайта, а также характера распределения кликов между ключевиками.
Например, если у нас мало кликов на сайте, то это повышает ошибку в вычислении m, и мы снижаем вес m. Если клики распределены неравномерно, например, в основном находятся у одного ключевика, то это тоже снижает точность m, и мы снижаем вес этой оценки.
Более точный прогноз ошибки повышает стабильность расчета А и точность оценки на малых данных.
Другие улучшения
Кроме использования REM модели есть еще следующие улучшения ПББ.
Дифференциация
В качестве m лучше использовать REM-оценку взятую не по всем ключевым словам, а по всем, кроме текущего. Благодаря этому мы не учитываем дважды одни и те же данные. Также это избавляет от завышения оценки А у небольших клиентов.
Однако дифференциация повышает время расчета вдвое. Она требует расчета 180 полигамма функция на 1 ключевик против 90 в случае ее отсутствия.
Максимум апостериори
А что если на сайте очень мало ключевых слов? В этом случае при вычислении А будет большая погрешность.
Как и в случае конверсии, при оценке А можно сделать среднее взвешенным двух оценок: того А, который получается максимумом правдоподобия, и того А, который в среднем наблюдаем у других клиентов.
Допустим у клиентов А в среднем равен 1,5. Если у клиента вообще нет данных, то можно сказать, что у него А около 1,5.
В теории мы можем дать неплохую оценку А, даже если у клиента вообще нет данных. На практике, естественно, нам нужен еще и m, для вычисления которого нужны хотя-бы 10–30 конверсий в статистике за несколько месяцев.
В более продвинутых версиях движков при оценке А используется кроме данных текущего клиента, распределение А у других клиентов. Это называется максимумом апостеори. В итоге на небольших данных возрастает стабильность вычислений А, на больших данных оценки этими двумя методами почти не отличаются.
Два периода
В оптимизаторах есть настройка период сбора статистики. Чем он выше тем больше у нас данных и тем меньше погрешность и выше прибыль. На первый взгляд этот период нужно увеличить.
Однако конверсия ключевых слов меняется во времени. Это происходит из-за сезонности, погоды, экономической ситуации, улучшений на сайте, рекламных акций и множества других факторов. Чем оперативнее мы реагируем на это, тем больше прибыли получим. Чтобы повысить оперативность, нужно сократить период сбора статистики.
Поэтому нужно искать компромиссную длину периода. Если период слишком короткий, то точность оценки будет невысокой. При слишком длинном периоде, система будет реагировать на изменения с очень большой задержкой.
В некоторых оптимизаторах ставок есть 2 периода. Благодаря основному (более длинному) мы получаем много данных, а благодаря вспомогательному (более короткому) мы оперативно реагируем на изменения.
Для больших сайтов можно выставить вспомогательный период в несколько недель, а основной – в полгода. Благодаря чему прогноз будет одновременно и точным, и оперативным.
Иерархия
Мы довольно легко можем сделать Бета-биномиальную модель иерархической. Чтобы она учитывала данные группы объявлений и кампании.
Сначала мы оцениваем конверсию кампании:
Потом вычисляем оценку конверсии группы объявления, используя вместо m оценку кампании.
После чего вычисляем оценку ключевого слова, используя оценку группы:
В конечном счете, эти формулы сводятся к средневзвешаному 4-х оценок: по сайту, кампании, группе и самому ключевику. Причем поскольку групп и кампаний намного меньше, чем ключевых слов, то ресуркоемкость расчета практически не увеличивается, если мы не будем использовать дифференциацию.
Однако иерархическая модель имеет и свои проблемы:
- Конверсия кампании и средняя конверсия ключевого слова кампании – это разные вещи. REM в рамках этой модели не решает проблему.
- Должна быть четкая иерархия. Мы не можем учитывать какие-то другие оценки вне иерархии, например по URL.
- Расчет A на последних уровнях становится не стабильным уже у средних клиентов.
Чтобы решить подобные проблемы требуется более сложная модель, которая требует уже намного большего объема вычислений.
Показатель отказов
В теории кроме прогноза по группам мы можем использовать и другие оценки. Самая важная из них это оценка по показателю отказов. Например, пусть b – это показатель отказов. Чем выше показатель отказов, тем меньше конверсия. Вот самый простой метод:
Например, m = 1%, а показатель отказов по сайту равен 60%, тогда k = 1%/(1-60%)=1%/40%=0,025=2,5%.
Допустим, у ключевика 80% отказов, тогда мы можем дать следующую оценку конверсии:
Допустим, у другого ключевика 30% отказов, тогда мы можем дать следующую оценку конверсии:
Эту модель можно понять благодаря воронке из трех шагов. Сначала идут клики, часть из них становится отказами. Оставшиеся клики (не отказы) с некоторой вероятностью (k) превращаются в конверсии.
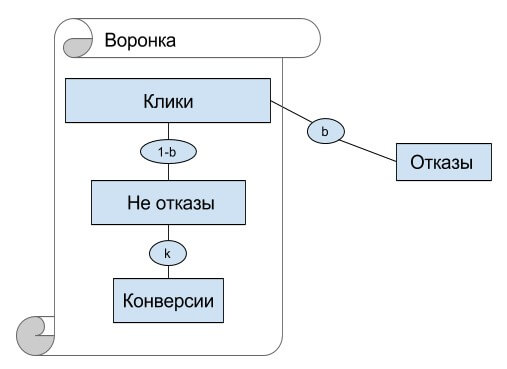
Чтобы рассчитать вес этой оценки, нужно оценить ее погрешность. Она состоит из двух компонентов. Пусть B это вероятность отказа, тогда
- Погрешность данных. Возникает из-за того, что вероятность отказа не равна показателю отказов. При увеличении числа кликов снижается вплоть до нуля на бесконечном объеме данных. Обычно в 5–20 раз ниже, чем у показателя конверсий.
- Систематическая погрешность возникает из-за того, что наша модель не абсолютно точна. Из-за того, что k у разных ключевых слов разное. Эта погрешность не зависит от объема данных. При бесконечном объеме данных суммарная погрешность была бы равна систематической.
Можно использовать более сложную модель, в которой есть еще и скрытые отказы, в ней систематическая погрешность невелика. Эта модель очень точно предсказывает промежуточные цели вроде добавления товара в корзину.
Ошибка данных тоже невелика. Обычно вероятность отказов в районе 50%, а конверсия 1%. В этом случае, если бы систематическая ошибка была нулевой, то наша формула при 10 кликах была бы такой же точной, как и показатель конверсии при 1000!
Если у ключевого слова будет очень мало кликов, то оценка по отказам будет хуже оценки по группам. Но с ростом числа кликов она будет быстро улучшаться (намного быстрее, чем показатель отказов) до тех пор, пока не достигнет систематической ошибки.
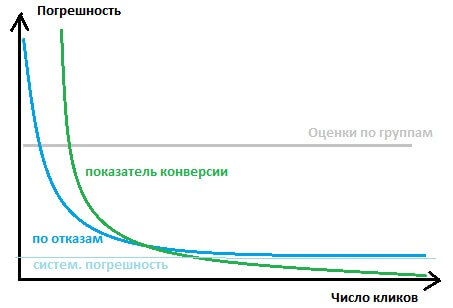
Обычно основная масса кликов у клиента приходится как раз на те ключевики, у которых не сильно много и не сильно мало кликов. У таких ключевиков лучше всего работает оценка по отказам, и поэтому оценка по отказам значительно повышает качество итоговой оценки.
В общем, несмотря на то что оценка по отказам только одна из многих, ее вклад в увеличение прибыли довольно высок.
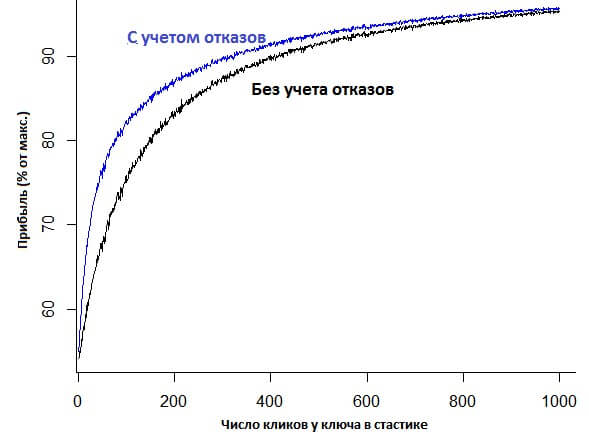
Как мы видим, при не сильно большом числе кликов, учет отказов значительно повышает прибыль.
Заключение
Оптимизаторы ставок оценивают конверсию по множеству факторов. Показатель конверсии один из них, но при маленьком числе кликов у ключевика его вклад в общую оценку будет незначительным.
Показатель конверсии обычно играет существенную роль только у высокочастотных ключевых слов, когда он довольно достоверно отражает конверсию.
При расчете конверсии используется среднее взвешенное нескольких оценок. Если какая-то из оценок имеет высокую погрешность (как показатель при малом числе кликов), то она просто берется с очень маленьким весом. Это не ухудшает оценку.



 Теги:
Теги:
